ĀNURŨPYENA
The upa-Sutra 'Anurupyena' means 'proportionality' or 'similarly'. This Sutra is highly useful to find products of two numbers when both of them are near the Common bases like 50, 60, 200 etc(multiples of powers of 10).
Example 1: 46 X 43
As per the previous methods, if we select 100 as base we get

This is much more difficult and of no use.
Now by ‘Anurupyena’ we consider a different working base through we can solve the problem.
Take the nearest higher multiple of 10. In this case it is 50.
Treat it as 100 / 2 = 50.
Now the steps are as follows:
i) Choose the working base near to the numbers under consideration.
i.e., working base is 100 / 2 = 50
ii) Write the numbers one below the other
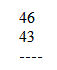
iii) Write the differences of the two numbers respectively from 50 against each number on right side
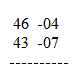
iv) Write cross-subtraction or cross- addition as the case may be under the line drawn. Multiply the differences and write the product in the left side of the answer.
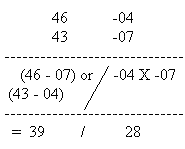
v) Since base is 100 / 2 = 50 , 39 in the answer represents 39X50.
Hence divide 39 by 2 because 50 = 100 / 2
Thus 39 ÷ 2 gives 19½ where 19 is quotient and 1 is remainder . This 1 as Reminder gives one 50 making the L.H.S of the answer 28 + 50 = 78(or Remainder ½ x 100 + 28 ) i.e. R.H.S. 19 and L.H.S. 78 together give the answer 1978.
We represent it as

Solve 58 x 48 :
Working base 50 = 5 x 10 gives
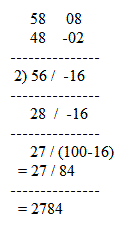
Find the following products.
1.46 x 46 2. 57 x 57 3. 54 x 45
Example 1: 46 X 43
As per the previous methods, if we select 100 as base we get

This is much more difficult and of no use.
Now by ‘Anurupyena’ we consider a different working base through we can solve the problem.
Take the nearest higher multiple of 10. In this case it is 50.
Treat it as 100 / 2 = 50.
Now the steps are as follows:
i) Choose the working base near to the numbers under consideration.
i.e., working base is 100 / 2 = 50
ii) Write the numbers one below the other
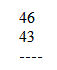
iii) Write the differences of the two numbers respectively from 50 against each number on right side
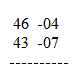
iv) Write cross-subtraction or cross- addition as the case may be under the line drawn. Multiply the differences and write the product in the left side of the answer.
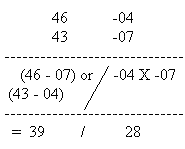
v) Since base is 100 / 2 = 50 , 39 in the answer represents 39X50.
Hence divide 39 by 2 because 50 = 100 / 2
Thus 39 ÷ 2 gives 19½ where 19 is quotient and 1 is remainder . This 1 as Reminder gives one 50 making the L.H.S of the answer 28 + 50 = 78(or Remainder ½ x 100 + 28 ) i.e. R.H.S. 19 and L.H.S. 78 together give the answer 1978.
We represent it as

Solve 58 x 48 :
Working base 50 = 5 x 10 gives
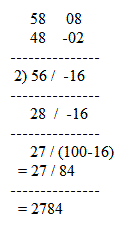
Find the following products.
1.46 x 46 2. 57 x 57 3. 54 x 45





0 Comments:
Post a Comment
<< Home